Initial Abstraction

Introduction

In hydrology, watershed runoff generation is a dynamic and complex hydrological process that plays an important role in the development of flood events. Understanding the relationship between rainfall and runoff is a key issue in the management and control of water resources.

The runoff is generated by the rainfall that remains after the losses that take place through evaporation, vegetation interception, surface depression storage, and infiltration. This loss of rainfall, including the processes of interception, infiltration, evaporation, and surface depression storage, during the period from the beginning of rainfall to the generation of runoff, is termed initial abstraction (Ia).

Calculation of Initial Abstraction (Ia)

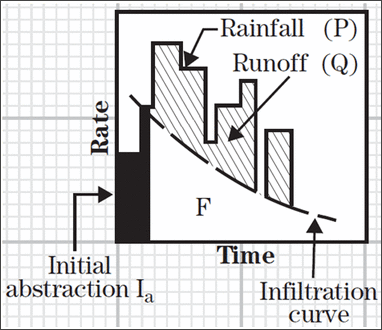
Initial abstraction (Ia) is a sensitive parameter in hydrological models, and its value directly determines the amount of runoff. Initial abstraction (Ia), which is affected by multiple factors related to antecedent watershed condition (AWC), is difficult to estimate due to a lack of observed data.

Though initial abstraction (Ia) is highly variable, it is correlated with soil and cover parameters. According to the Soil Conservation Service Curve Number (SCS Curve Number) method and studies from various agricultural watersheds, the initial abstraction (Ia) is found to be approximated by the following equation:

Initial abstraction (Ia) = 0.2 x S (where S= potential maximum retention after runoff begins (in))

Note that this approximation can be important exclusive of an urban application because the combination of impervious areas with pervious areas might result in a considerable initial loss that may not occur. If impervious areas feature surface depressions that store some runoff, the opposite effect can occur, resulting in a greater initial loss.

Determining SCS Runoff Curve Number Using Initial Abstraction (Ia)

The value of initial abstraction (Ia) is related to climatic and watershed antecedent wetness conditions. The estimation of initial abstraction (Ia) is of great significance in determining runoff, which influences flood management and forecast.

The SCS Runoff Curve Number method, proposed by the United States Department of Agriculture (USDA) Soil Conservation Service (SCS), is most widely used because of its lower input parameters and simple structure. Soil texture, topographic factors, vegetation condition, and land use of the watershed are considered, which makes the SCS Runoff Curve Number method suitable for the estimation of runoff for long-term gauged watersheds as well as ungauged watersheds.

The equation for the SCS Runoff Curve Number method is as follows:

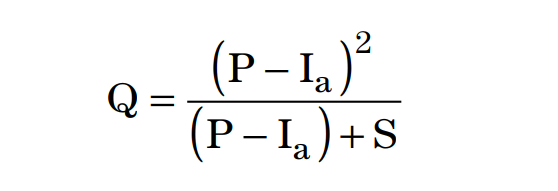
Where:

Q = Runoff (in)
P = Rainfall (in)
S = Potential maximum retention after runoff begins (in)
Ia = Initial abstraction (in) = 0.2 x S

By removing initial abstraction (Ia) as an independent parameter, this calculation allows the use of a combination of “S” and “P” to produce a unique runoff amount.

Therefore, the above equation can be written as:

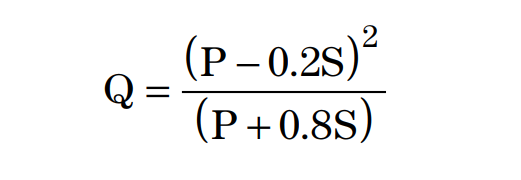
Here, “S” specifies the potential maximum retention after runoff begins (in), a measure of the ability of a watershed to abstract and retain storm precipitation. It is related to the soil and cover conditions of the watershed through the SCS Runoff Curve Number, which has a range from 0 to 100. Therefore, “S” is related to the SCS Runoff Curve Number by:

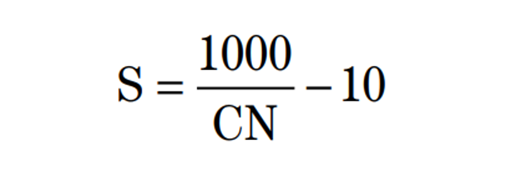
Note that for the metric (SI) unit of measurement system, the equation “S” can be written as:

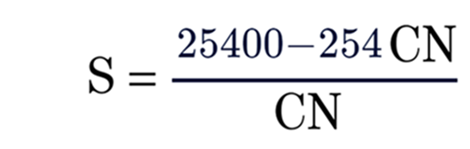
The graphical representation of the direct runoff (Q) and rainfall (P) to solve the SCS runoff equations can be seen in the below figure.

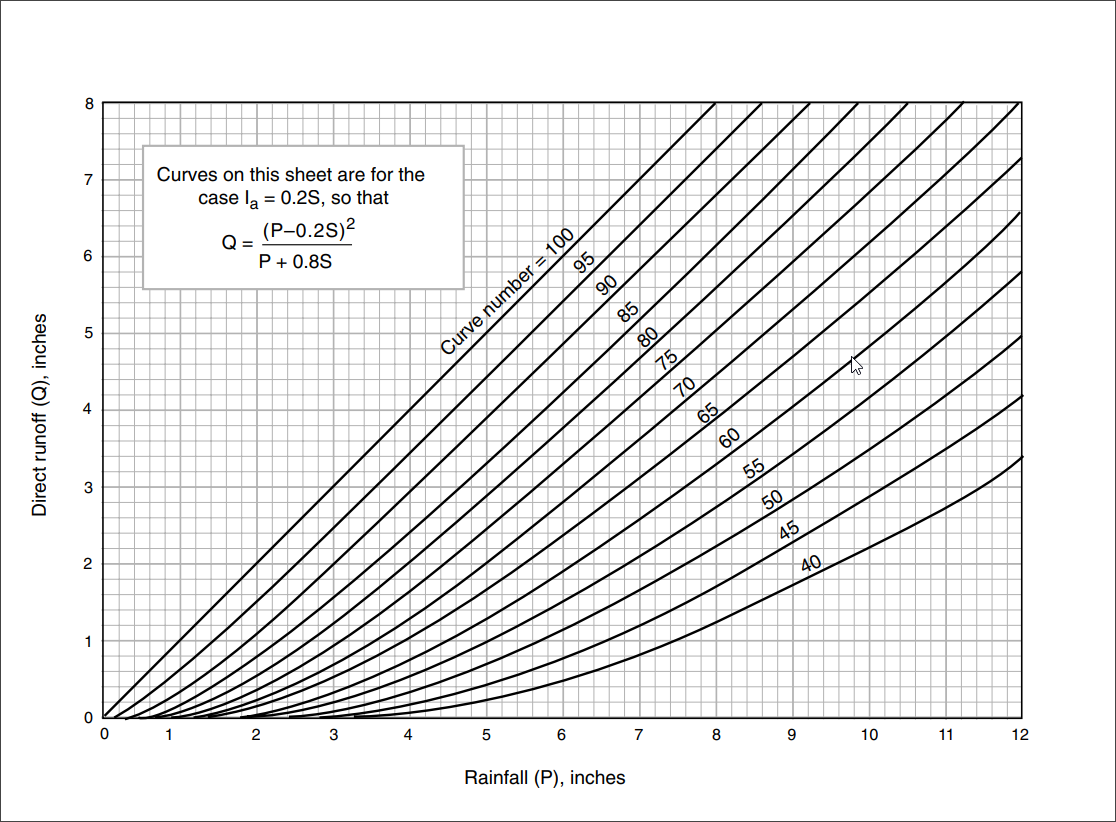
The runoff depth for selected curve numbers and rainfall amounts can be seen in the below figure.

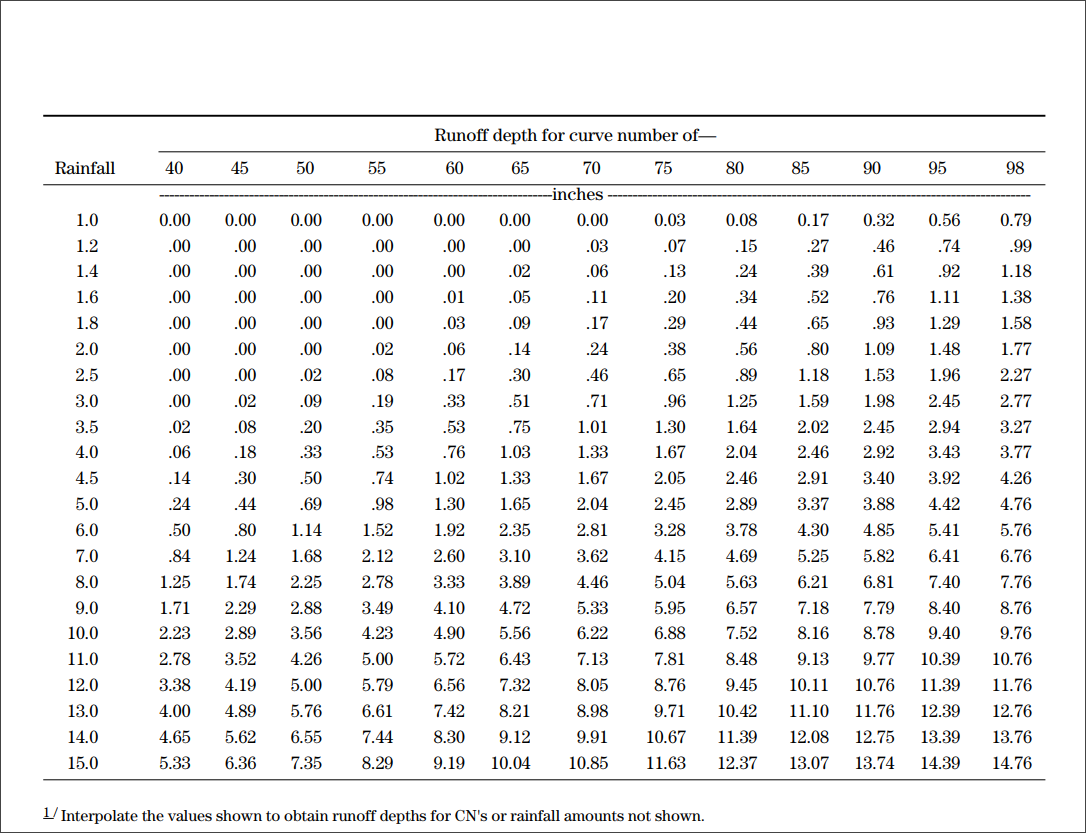
When the drainage area consists of land use with impervious cover (directly connected or unconnected), separate graphs for computing the composite curve number values can be used depending on the percent of the impervious cover. To learn more about the various graphs that can be used for computing the composite curve number, refer to TR-55 (Urban Hydrology for Small Watersheds). However, it is a good practice to compute the runoff from impervious and pervious areas separately and then add the volume.

The graphical representation for composite CN with connected impervious area can be seen in the below figure.

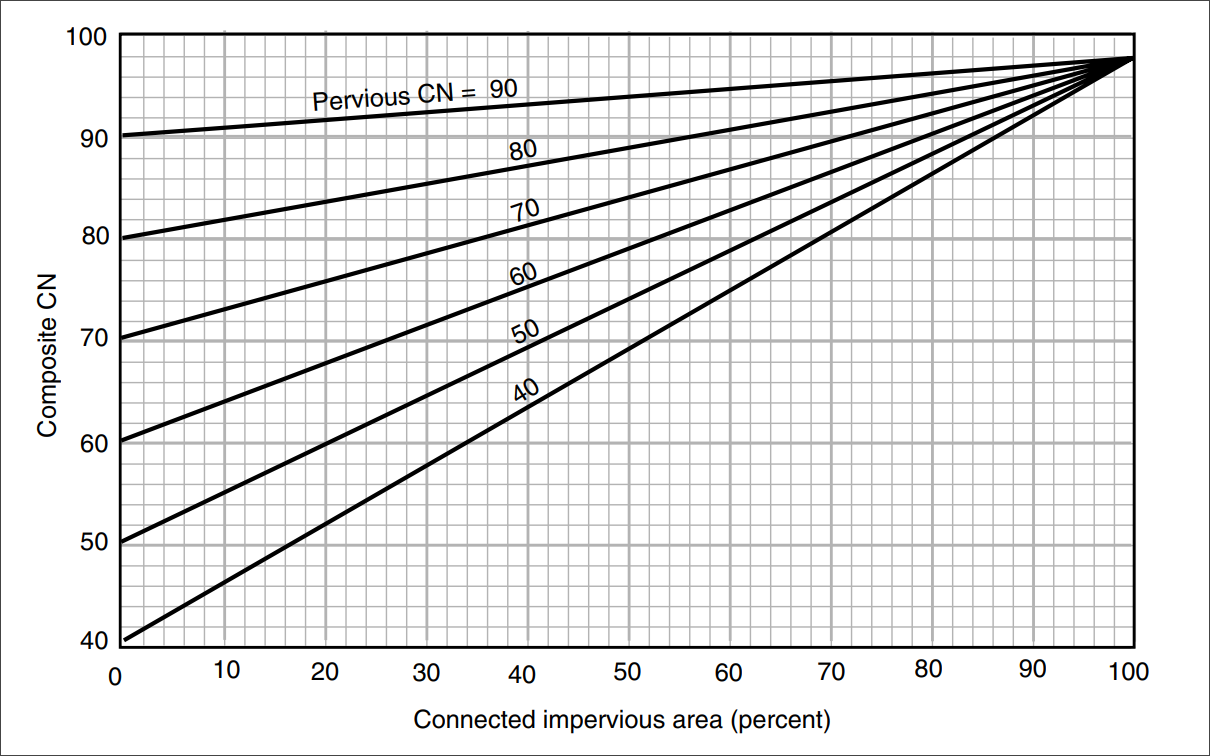
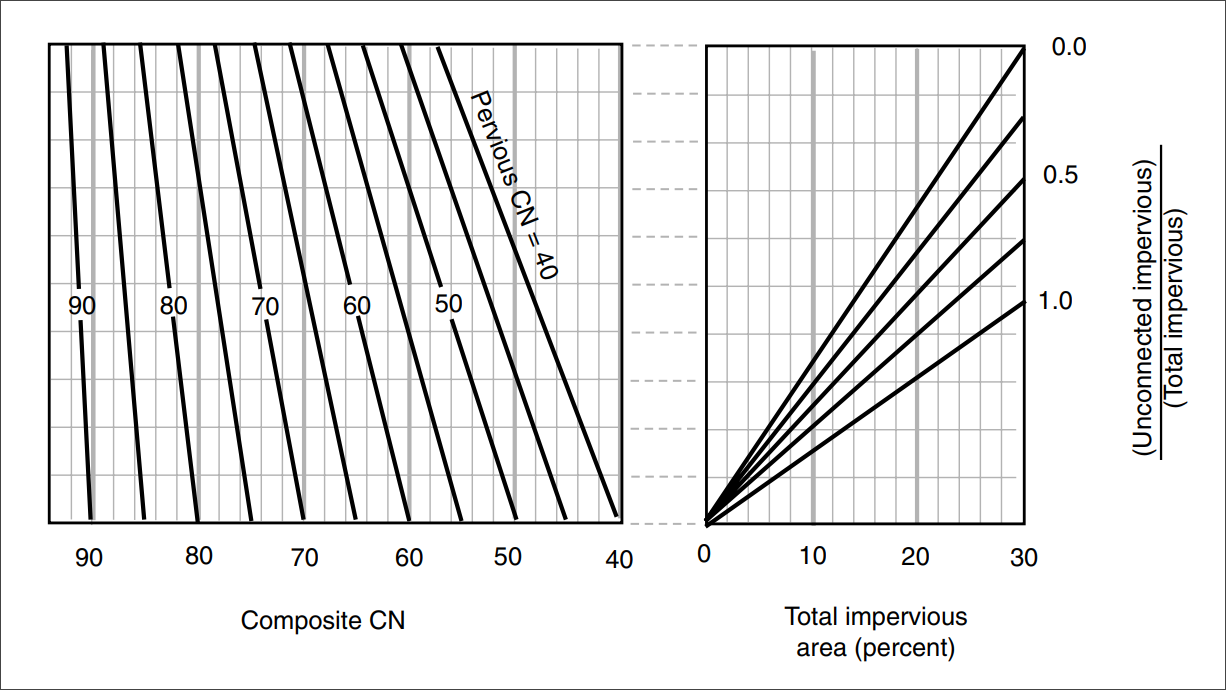
The graphical representation for composite CN with unconnected impervious areas and a total impervious area of less than 30% can be seen in the below figure.

To learn more about the SCS Runoff Curve Number approach and the criteria utilized in determining the runoff curve number, refer to the information available in TR-55 (Urban Hydrology for Small Watersheds).

Factors Affecting the Initial Abstraction (Ia)

The factors influencing initial abstraction (Ia) are collected from rainfall-runoff events. The driving factors affecting initial abstraction (Ia) vary across different watersheds and river basins.

Some of the factors that may impact the initial abstraction (Ia) value are as follows: